'Pure' musical note simplification

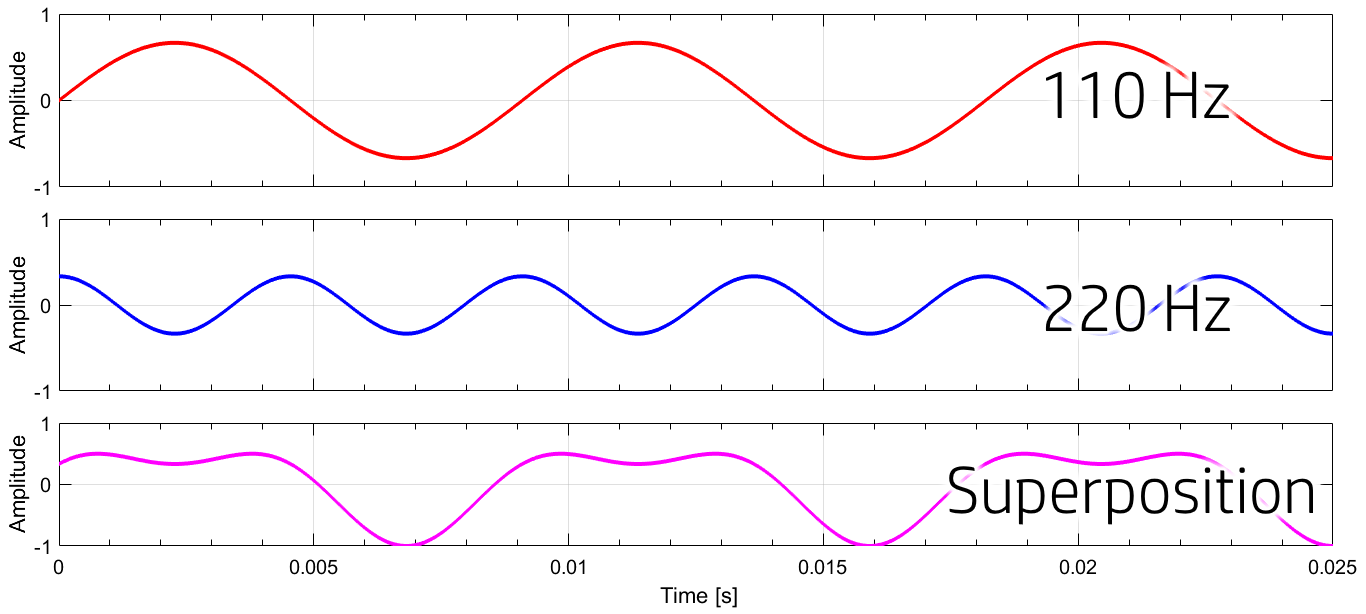
You may know that each note you play on the guitar is dominated by its fundamental frequency, \(f_0\) and is accompanied by higher frequency (higher pitched) overtones (or harmonics) occurring at integer multiples of the fundamental frequency (\(f_n=(n+1)×f_0\)) and are present with a lower amplitude than the fundamental frequency. All these components additively combine to create a single waveform (superposition). To put it another way, the sound that we hear can be broken up into some number of sinusoidal waveforms of varying frequencies and amplitudes. In the image below, the bottom plot shows a superposition of two waves with frequencies of \(110 Hz\) and \(220 Hz\).

To help visualise all of this, an Audacity analysis of an open A string recording follows.

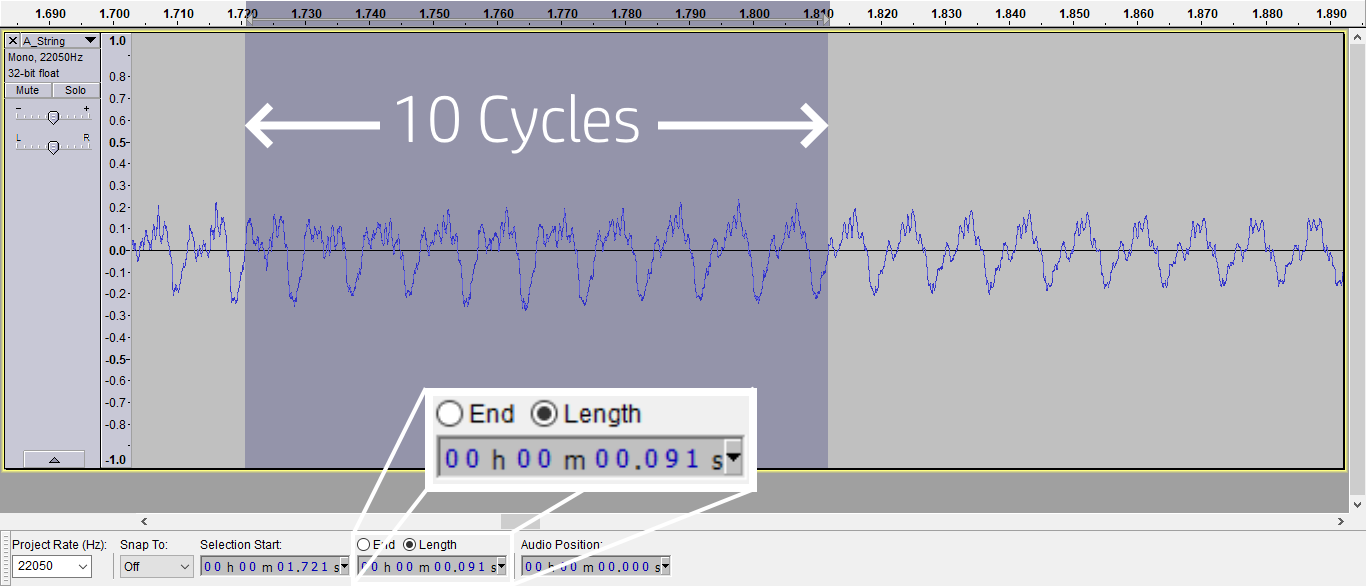
The first image below shows a portion of the waveform of the recording. There is a general periodicity to the signal, though you can clearly see the shape of the wave changing over time. This is a result of the harmonic content of the note changing over time. The duration for 10 cycles of this waveform is measured to be \(T_{10}=0.091s\). Averaging this result over ten cycles gives the duration of a single cycle, \(T={T_{10} \over 10}=0.0091s\). Now, frequency is simply defined as \(f={1 \over T}\), and so the (dominant) frequency of this signal is \(f={1 \over 0.0091}≈110Hz\), as we expect for an open A string.

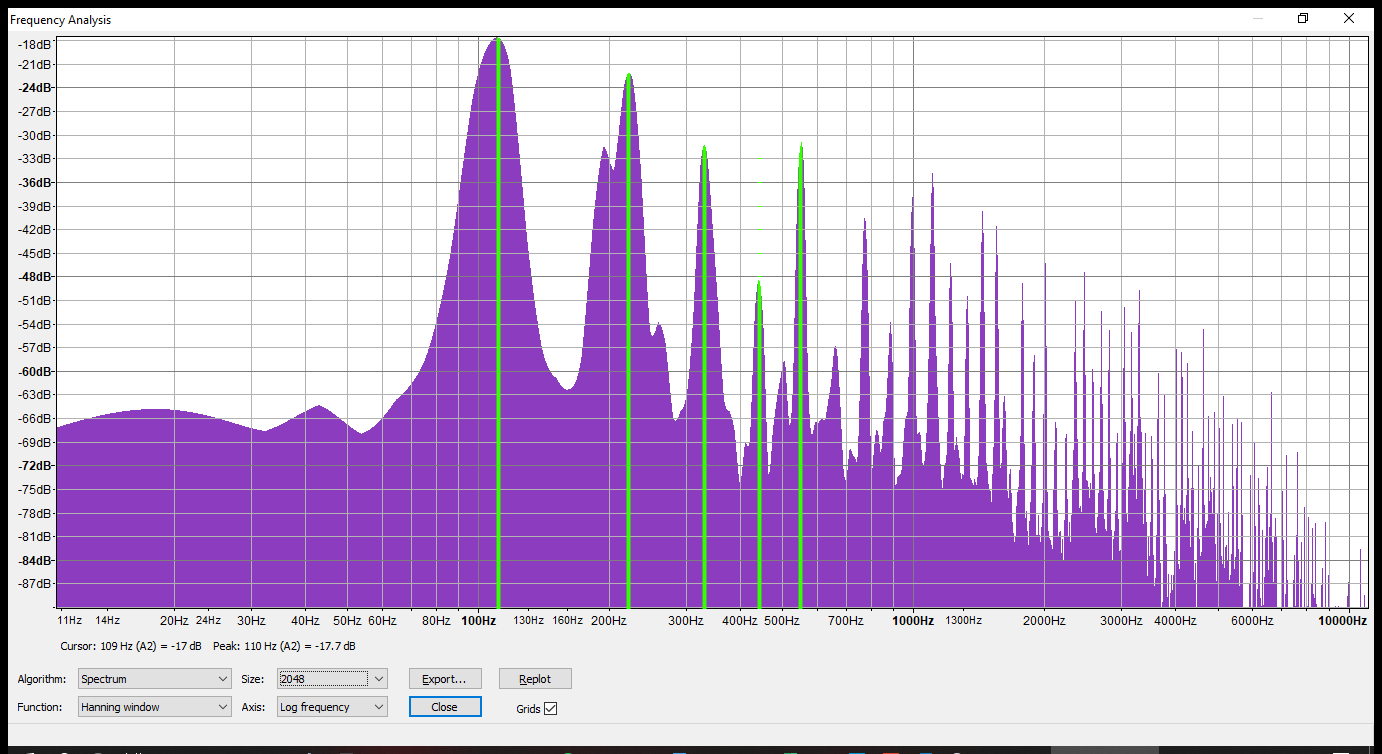
The second image shows the frequency analysis of this same audio signal (using Audacity’s Analyze > Plot Spectrum tool). This may or may not make sense to you, but the key points are that the horizontal axis represents frequency (in \(Hz\)), and the vertical axis represents the magnitude (in \(dB\)). Remember how we said we could split the audio signal into different frequency components - each with different magnitudes? This tool does that for us. In this case, the first 5 peaks are highlighted. They correspond to the fundamental frequency (\(f_0=110Hz\)), followed by the overtones we would expect for this note (\(f_1=220Hz\), \(f_2=330Hz\), \(f_3=440Hz\), \(f_4=550Hz\)).

This might all make you a bit itchy… Especially with an eye on our future of trying to design a circuit that can manipulate this kind of signal in some way. Don’t worry. We will apply the following simplifications that should make things a lot easier:

• Assume the audio signal is a perfect sinusoid.
• Assume the audio signal is of a single (fundamental) frequency, with no overtones. We will use \(f_0=110Hz\) as our default, which corresponds to the open A string.
• The amplitude of the signal remains constant over time, with no decay.

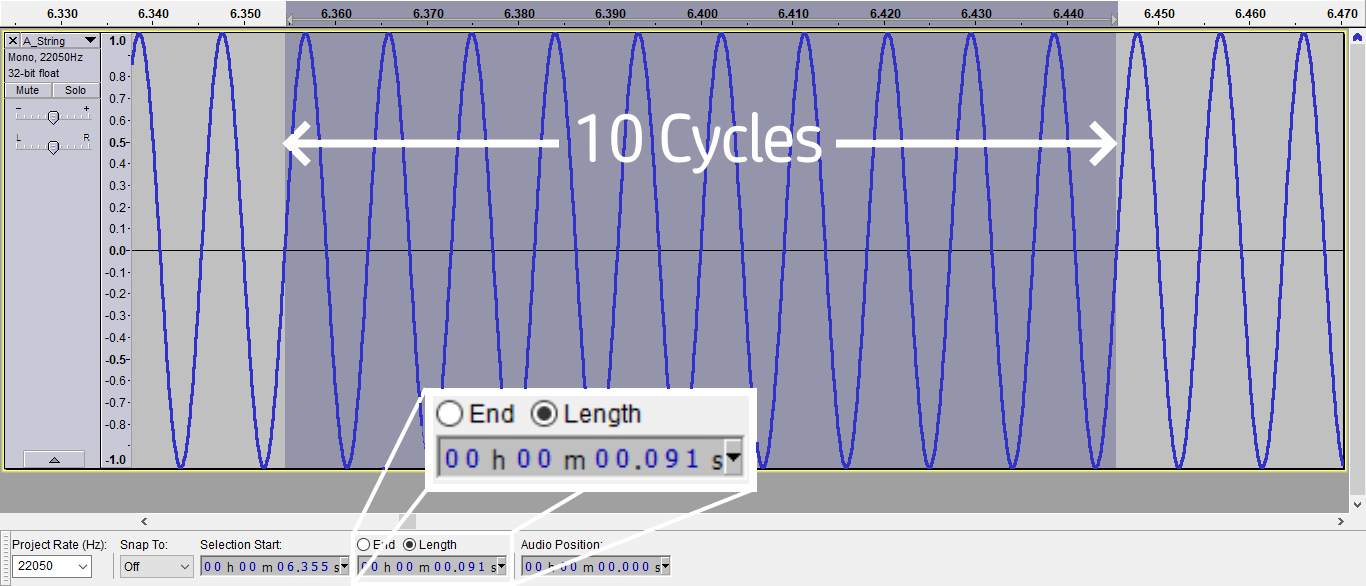
Our simplified audio signal is shown below (and a recording of what this sounds like). The frequency is still \(f_0=110Hz\), but we have eliminated the harmonics and any time variance in the signal. This will prove much simpler to analyse, and it turns out that it’s a good enough approximation to allow us to do a good job.

Signal Flow Simplification

Focussing on a single pedal design at a time, we will assume the chain of events is as follows:

Guitar Output → Effects Pedal → Amplifier Input

We already touched on pickups, but for all that follows, they’re not an important part of the signal chain. The same is true at the other end, and we don’t really care what happens once the signal has entered the amplification stage.
Later, we'll discuss the effects that the guitar output and the amplifier input have on our signal, but for now just know that our scope is limited only to the elements listed above, and so you don't need to go and worry about amplifiers and speakers (unless you really want to!).